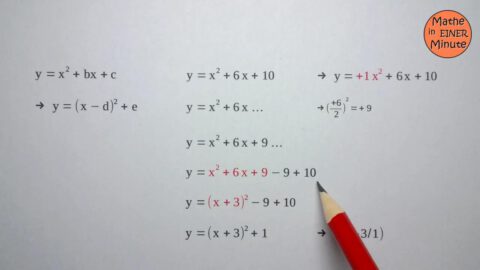901 – Quadratische Ergänzung / Normalparabel – Verständnis
Die Umformung einer Normalparabel aus der Normalform in die Scheitelform. Schritt für Schritt … durch quadratische Ergänzung.
095 – Spiegelung einer Funktion an der y-Achse 2 – Beispiel
Ein Beispiel zur Spiegelung einer Funktion an der y-Achse. Hier siehst du, wie man den Term der daraus hervorgehenden Funktion bestimmen kann.
094 – Spiegelung einer Funktion an der y-Achse 1 – Beispiel
Ein Beispiel zur Spiegelung einer Funktion an der y-Achse. Hier siehst du, wie man den Term der daraus hervorgehenden Funktion bestimmen kann.
093 – Spiegelung einer Funktion an der y-Achse – Verständnis
Die Spiegelung einer Funktion an der y-Achse. Hier erfährst du, was dabei passiert und wie man zum Term der daraus entstehenden Funktion kommt.
092 – Spiegelung einer Funktion an der x-Achse 2 – Beispiel
Ein Beispiel zur Spiegelung einer Funktion an der x-Achse. Hier siehst du, wie man den Term der daraus hervorgehenden Funktion bestimmen kann.
091 – Spiegelung einer Funktion an der x-Achse 1 – Beispiel
Ein Beispiel zur Spiegelung einer Funktion an der x-Achse. Hier siehst du, wie man den Term der daraus hervorgehenden Funktion bestimmen kann.
090 – Spiegelung einer Funktion an der x-Achse – Verständnis
Die Spiegelung einer Funktion an der x-Achse. Hier erfährst du, was dabei passiert und wie man zum Term der daraus entstehenden Funktion kommt.
089 – Streckung einer Funktion in x-Richtung 2 – Beispiel
Ein Beispiel zur Streckung (Stauchung) einer Funktion in x-Richtung. Hier siehst du, wie man den Term der daraus hervorgehenden Funktion bestimmen kann.
088 – Streckung einer Funktion in x-Richtung 1 – Beispiel
Ein Beispiel zur Streckung (Stauchung) einer Funktion in x-Richtung. Hier siehst du, wie man den Term der daraus hervorgehenden Funktion bestimmen kann.
087 – Streckung einer Funktion in x-Richtung – Verständnis
Die Streckung (Stauchung) einer Funktion in x-Richtung. Hier erfährst du, was dabei passiert und wie man zum Term der daraus entstehenden Funktion kommt.